The normalised cut algorithm

The normalised cut algorithm [88] can cluster a set of elements based only on the values of a similarity measure between all possible pairs of elements. The approach is a spectral clustering method. It is based on the properties of eigenvectors from a matrix computed using the similarities between each pairs of elements.

In the normalised cut scheme, the clustering is seen as a graph partitioning problem. The nodes of the graph are the elements and the weights on the graph edges connecting two nodes are the similarities measured between the two corresponding elements. We use the similarity measure described in the previous section. We seek to partition the graph into subgraphs with high similarities between the nodes of the same subgraphs and a low similarities between nodes from different subgraphs.

Let $G$ be that graph with nodes $V$ and an adjacent graph weight matrix $W$. The element $W(u,v)$ of $W$ is the similarity measured between the elements represented by the nodes $u$ and $v$. We can break $G$ into two disjoint sets $A$ and $B$ so that $A \cup B=V$ and $A \cap B= \emptyset$ by simply removing the edges connecting the two parts. The cost of removing those edges is computed as the total weight of the edges that have been removed:

$$cut(A,B)=\sum_{u \in A, v \in B}W(u,v)$$ (43)

This cost is called a ``cut'' in the graph theory language. We want to minimise this cut value when partitioning $G$.

However, minimising the cut value encourages cutting isolated nodes in $G$. To avoid that problem, the cost of removing edges from $A$ to $B$ is considered as a fraction of the total weight of connections from nodes in $A$ to all nodes in the graph. This leads to a new cost measure called the normalised cut:

$$Ncut(A,B)=\frac{cut(A,B)}{asso(A,V)}+\frac{cut(A,B)}{asso(B,V)}$$ (44)

where $asso(A,V)=\sum_{u \in A, v \in V}W(u,v)$ is the total connection weight from all the nodes in $A$ to all the nodes in $V$. $asso(B,V)$ is defined in a similar way. Our aim is now to find a partition of $G$ that minimise the normalised cut between the two parts.

Let ${\bf x}$ be a $\vert V\vert$ dimensional vector, that represents the partition of $V$ into two sets $A$ and $B$. $x_i=1$ if the node $i$ is in $A$ and $x_i=-1$ if the node $i$ is in $B$. We define:

$$Ncut({ {\bf x} })=Ncut(A,B)$$ (45)

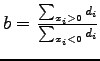Let $d_i=\sum_{j \in V} W(i,j)$, the total weight of edges between the node $i$ and all the other nodes in the graph. Let $D=diag\left(d_i\right)$ and let $b=\frac{\sum_{x_i>0}d_i}{\sum_{x_i<0}d_i}$. It is proven in [87] that:

$$\min_{{\bf x} }Ncut( {\bf x} )=\min_{{\bf y} }\frac{{{\bf y}}^T(D-W){{\bf y}}}{{{\bf y}}^T D{{\bf y}}}$$ (46)

subject to the constraints $y_i \in \{1,-b\}$ and ${\bf y }^T D {\bf 1} = 0$. The change of variable:

$${\bf y}=\frac{{\bf 1}+{\bf x}}{2}-b\frac{{\bf 1}-{\bf x}}{2}$$ (47)

has been used. So $y_i = 1$ if the node $i$ is in $A$ and $y_i = -b$ if the node $i$ is in $B$.

$\frac{{{\bf y}}^T(D-W){{\bf y}}}{{{\bf y}}^T D{{\bf y}}}$ is called the Rayleigh quotient [36,63]. The minimisation of equation B.4 can be approximate by relaxing ${\bf y}$ to take real values and solving the generalised eigenvalue system:

$$(D-W){\bf y}=\lambda D{\bf y}$$ (48)

Equation B.6 can be rewritten as a standard eigensystem:

$$D^{-\frac{1}{2}}(D-W)D^{-\frac{1}{2}}{\bf z}=\lambda {\bf z}$$ (49)

with ${\bf z}=D^{-\frac{1}{2}}{\bf y}$.

By observing the following:

• $D^{-\frac{1}{2}}(D-W)D^{-\frac{1}{2}}$ is a symmetric diagonally dominant real matrix with non-negative diagonal entries so it is positive semidefinite; it has therefore only positive eigenvalues
• $D^{-\frac{1}{2}}{\bf 1}$ is an eigenvector of $D^{-\frac{1}{2}}(D-W)D^{-\frac{1}{2}}$; its corresponding eigenvalue is $0$
• $D^{-\frac{1}{2}}(D-W)D^{-\frac{1}{2}}$ is symmetric so its eigenvectors are orthogonal to each other, in particular the eigenvector $z_1$ that corresponds to the second smallest eigenvalue is orthogonal to $D^{-\frac{1}{2}}{\bf 1}$ and thus satisfy the constraint ${\bf y_1}^T D{\bf 1}=0$ with ${\bf z_1}=D^{\frac{1}{2}}{\bf y_1}$

we can use the following theorem [63]: Let $A$ be a $n \times n$ real symmetric matrix with eigenvalues $\lambda_1 \leq \lambda_2 \leq \ldots \leq \lambda_n$. The Rayleigh quotient $\frac{{\bf x}^T A {\bf x}}{{\bf x}^T {\bf x}}$ is minimised by the $j^{th}$ eigenvector, under the constraint that ${\bf x}$ is orthogonal to the eigenvector associated with the $j-1$ smallest eigenvalues of $A$. The minimum is equal to the $\lambda_j$.

In our case, we can conclude that ${\bf z_1}$ minimises $\frac{{\bf z}^T D^{-\frac{1}{2}}(D-W)D^{-\frac{1}{2}} {\bf z}}{{\bf z}^T {\bf z}}$ under the constraint ${\bf z}^T D^{\frac{1}{2}} {\bf 1} = 0$. So, ${\bf y_1} = D^{-\frac{1}{2}} {\bf z_1}$ minimises $\frac{{\bf y}^T (D-W) {\bf y}}{{\bf y}^T {\bf y}}$ under the constraint ${\bf y }^T D {\bf 1} = 0$.

We need only to compute the eigenvector associated with the second smallest eigenvalue. We use the Lanczos algorithm to compute that vector. This algorithm iteratively approximates the eigenvectors until convergence [36]. In contrast to singular value decomposition, only two eigenvectors have to be computed to get the eigenvector we are looking for. This makes the Lanczos algorithm quicker, especially for large matrices.

The solution $\bf {y_1}$ of the relaxed problem can be used as an approximate solution to the original discrete problem. We need an extra condition on the components of the solution $\bf {y_1}$: $y_i \in \{1,-b\}$. In the ideal case, the components of the eigenvector takes only two discrete values, which represents the two classes. If it is not the case, we need to choose a splitting point to partition the values of the components of the eigenvector. Here we simply choose $0$ as a splitting point. All the positive components represent elements from one class and all the negatives ones represent elements from the other class. Other methods exist for choosing the splitting point [89].

We can then separate the set of elements into two sets, one containing the elements corresponding to positive values in the eigenvector and the other one containing elements corresponding to negative values in the eigenvector. We recursively cluster the resulting two element sets until we reach a given number of clusters.

This number of resulting clusters is usually not a power of two as one would expect given our description of the algorithm. This is due to the fact that the normalised cuts algorithm does not always separate the groups into two for each steps. It is possible that the second eigenvector given by the Lanczos algorithm has only positive or only negative values. This can be due either to rounding errors in the computation of the eigenvector or to cases where the choice of $0$ as a threshold value for selecting the two groups is a bad choice (the solution of the normalised cuts algorithm is only an approximation of the continuous case). It can also be due to the fact that the group we are trying to split only contains one element (due to previous splits). In that case, we do not split the group so the count of the number of group will not be a power of two.