



Next: Conclusion
Up: Quantitative assessment of the
Previous: Performance given a large
Index
The test was repeated training on the shortest text 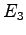 . Results are reported in tables 6.2 and 6.3 for the Matusita distance and the KL divergence respectively.
. Results are reported in tables 6.2 and 6.3 for the Matusita distance and the KL divergence respectively.
Table 6.2:
Comparison of the prediction of a VLMM learnt from a short text using the Matusita distance. The VLMM has been trained using the text 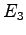 . It has been tested on the three texts
. It has been tested on the three texts  ,
, 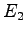 and
and 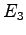 . The results are reported for Lidstone's law of sucession for different values of
. The results are reported for Lidstone's law of sucession for different values of 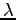 . The case
. The case 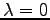 corresponds to the maximum likelihood estimate. The case
corresponds to the maximum likelihood estimate. The case 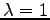 , which corresponds to Laplace's law of sucession, completely failed since it only predicted spaces.
, which corresponds to Laplace's law of sucession, completely failed since it only predicted spaces.
|
|
Table 6.3:
Comparison of the prediction of a VLMM learnt from a short text using the Kullback-Leibler divergence. The VLMM has been trained using the text 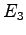 . It has been tested on the three texts
. It has been tested on the three texts  ,
, 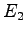 and
and 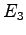 . The results are reported for Lidstone's law of sucession for different values of
. The results are reported for Lidstone's law of sucession for different values of 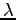 . The case
. The case 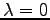 corresponds to the maximum likelihood estimate. The case
corresponds to the maximum likelihood estimate. The case 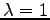 corresponds to Laplace's law of sucession.
corresponds to Laplace's law of sucession.
|
|
The method using the KL divergence performs better this time. Associated with the Laplace's law of succession, it is able to predict about  of a text dealing with another subject (
of a text dealing with another subject ( and
and 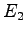 ).
).
In the case of the Matusita distance, the best performance is achieved with 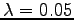 . It seems that this time, the maximum likelihood estimate could not explain the data on its own. A small amount of uniform prior was important. This is due to the fact that there were insufficient training data. We cannot trust the frequencies counted in the training sequence as we could with the training on a large dataset, so we need to include a part of uniform estimation which is done by increasing the value of
. It seems that this time, the maximum likelihood estimate could not explain the data on its own. A small amount of uniform prior was important. This is due to the fact that there were insufficient training data. We cannot trust the frequencies counted in the training sequence as we could with the training on a large dataset, so we need to include a part of uniform estimation which is done by increasing the value of 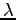 .
.




Next: Conclusion
Up: Quantitative assessment of the
Previous: Performance given a large
Index
franck
2006-10-01
![]() . Results are reported in tables 6.2 and 6.3 for the Matusita distance and the KL divergence respectively.
. Results are reported in tables 6.2 and 6.3 for the Matusita distance and the KL divergence respectively.
![]() of a text dealing with another subject (
of a text dealing with another subject (![]() and
and ![]() ).
).
![]() . It seems that this time, the maximum likelihood estimate could not explain the data on its own. A small amount of uniform prior was important. This is due to the fact that there were insufficient training data. We cannot trust the frequencies counted in the training sequence as we could with the training on a large dataset, so we need to include a part of uniform estimation which is done by increasing the value of
. It seems that this time, the maximum likelihood estimate could not explain the data on its own. A small amount of uniform prior was important. This is due to the fact that there were insufficient training data. We cannot trust the frequencies counted in the training sequence as we could with the training on a large dataset, so we need to include a part of uniform estimation which is done by increasing the value of ![]() .
.