Since only two choices are available for each question, the statistics of the set of answers describe a binomial distribution. If we are comparing videos generated from a model A with videos generated from a model B, the probability ![]() of choosing the videos generated by the model A
of choosing the videos generated by the model A ![]() times out of
times out of ![]() trials is given by the equation:
trials is given by the equation:
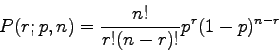 |
(40) |
We want to answer the question: "can people distinguish between two different models by looking at generated videos from the two models"?
We consider the null hypothesis that the videos are indistinguishable. In this case, ![]() and the distribution of
and the distribution of ![]() is given by:
is given by:
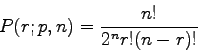 |
(41) |
We reject the null hypothesis if:
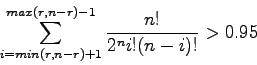 |
(42) |
i.e. there is a ![]() chance that we would have obtained a smaller difference if the videos had been indistinguishable.
chance that we would have obtained a smaller difference if the videos had been indistinguishable.
Similar equations can be used to check whether people prefer the left or the right when choosing videos from two choices extracted from the original sequence.