The Kullback-Leibler divergence

This measure of distance between probabilities is well known in the area if information theory. Let $p$ and $q$ describe two measure of probabilities, the Kullback-Leibler divergence is given by :

$$D_{KL}(p\Vert q)=\int p(x) \ln \left( \frac{p(x)}{q(x)} \right) \; dx$$

where the variable $x$ describe the entire space. As here we have modeled the probabilities $\tilde{P}$ by discrete values on a known alphabet $\Sigma$, we have:

$$D\left(\tilde{P}(\cdot\vert\sigma s)\Vert\tilde{P}(\cdot\vert... ...lde{P}(\sigma'\vert\sigma s)}{\tilde{P}(\sigma'\vert s)}\right)$$

Thus :

$$Err(\sigma s,s)=\sum_{\sigma'\in \Sigma}\tilde{P}(\sigma s \s... ...')\tilde{P}(s)}{\tilde{P}(\sigma s)\tilde{P}(s \sigma')}\right)$$

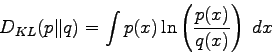
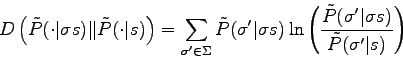
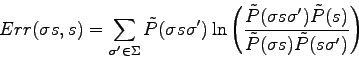
This measure of a distance between probabilities has been used in [51] together with the Laplace's law of succession in order to correct corrupted texts using a variable length Markov model.

We can also notice in the computation of the error measure, that the sum has $\vert\Sigma\vert$ terms and so the computation of a distance measure is computationally expansive.