The Matusita distance

We have also tested to the use of the Matusita measure instead of the Kullback-Leibler measure as advised by [1]. The Matusita measure between two probability distributions $p$ and $q$ is given by :

$$D_{B}(p\Vert q)=\int \left(\sqrt{p(x)}-\sqrt{q(x)}\right)^2 \; dx = 2-2\int \sqrt{p(x)\cdot q(x)} \; dx$$

where $x$ describe the whole space again. The term 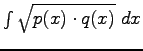$\int \sqrt{p(x)\cdot q(x)} \; dx$ is called the Bhattacharyya measure. In our case the distance becomes :

$$D\left(\tilde{P}(\cdot\vert\sigma s)\Vert\tilde{P}(\cdot\vert... ...{\tilde{P}(\sigma'\vert\sigma s)\cdot\tilde{P}(\sigma'\vert s)}$$

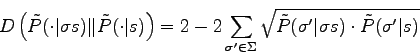
Thus :

$$Err(\sigma s,s)=2\tilde{P}(\sigma s) - 2\tilde{P}(\sigma s)\s... ...\sigma')\tilde{P}(s \sigma')}{\tilde{P}(\sigma s)\tilde{P}(s)}}$$

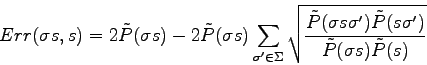
We can notice that the computation of the Matusita measure also requires to sum $\vert\Sigma\vert$ terms so the two measure of distance are computationally equivalent. However, the Bhattacharyya term has nice properties such as being symmetrical or being invariant to scale in the case of two Gaussian probability density distributions. The Matusita measure inherits of these properties.