Comparison of learnings using the Kullback-Leibler divergence

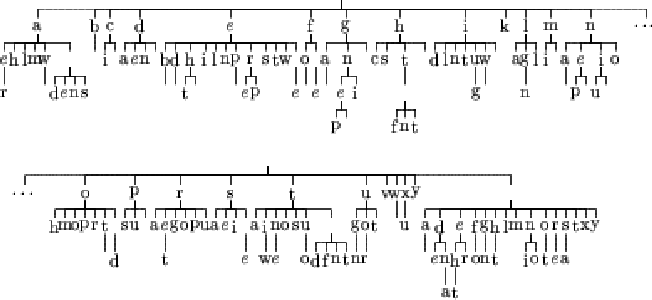
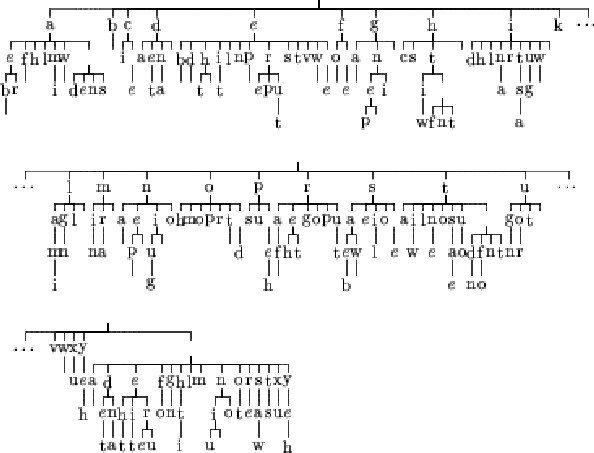
We kept the same text to train the variable length Markov model, but this time, the KL divergence was used. Figures 6.5, 6.6 and 6.7 show the resulting trees.

Figure 6.5: VLMM tree learned using the maximum likelihood estimation of probability and the Kullback-Leibler divergence. $\epsilon$ is set to 0.003 and only the probabilities that are greater than 0.003 are shown on the graph.

Figure 6.6: VLMM tree learned using the Lidstone estimation of probability with $\lambda =0.5$ and the Kullback-Leibler divergence. $\epsilon$ is set to 0.003 and only the probabilities that are greater than 0.003 are shown on the graph.

Figure 6.7: VLMM tree learned using the Laplace estimation of probability and the Kullback-Leibler divergence. $\epsilon$ is set to 0.003 and only the probabilities that are greater than 0.003 are shown on the graph.

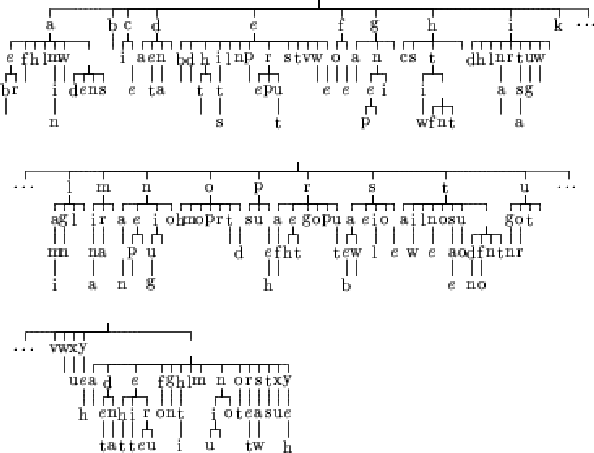We can see that this time, the estimation of probability used seems to exert less influence on the result. We can notice that, for the case of the maximum likelihood estimate, the tree does not change a lot compared to the corresponding case in the previous section. The two other trees have grown.

The aim of the variable length Markov model is to reduce the number of links we need to store in order to model the probability distribution. The size of the tree influences directly the learning because the more nodes there are in the tree, the more nodes the learning algorithm has to check. So it is possible that the KL divergence gives us a less efficient tree.

Due to the small amount of data used to construct these trees, the learning using the KL divergence in the two last cases can simply give such a tree because the text has been over learned. In order to make sure that it is not the case, another experiment has been done in the next section.