Conclusion

This chapter described the results found when we have investigated the use of variable length Markov model. It has been shown that the use of the Matusita distance in the learning algorithm and the use of the maximum likelihood produced the best estimates of the probability distribution. However, if the number of data used to train the VLMM is too small, then we do not want to trust totally the observed data, thus a combination of Kullback-Leibler divergence and Laplace's law of succession is better. This is conform to what has been observed in rule sets learning with the use of the $m$-estimate of rule accuracy given by:

$$\frac{n_s+m p}{N_s+m}$$

where $p$ is a prior and $m$ a weight [45]. The $m$-estimate is equivalent to a Lidstone estimate if we take :

$$p=\frac{1}{\vert\Sigma\vert}$$

and

$$m=\lambda \vert\Sigma\vert$$

So the result is not surprising.

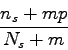
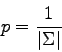
It has also been shown how the number of tests we have to do before finding the correct element in a sequence can involve on accuracy.