Other generative methods

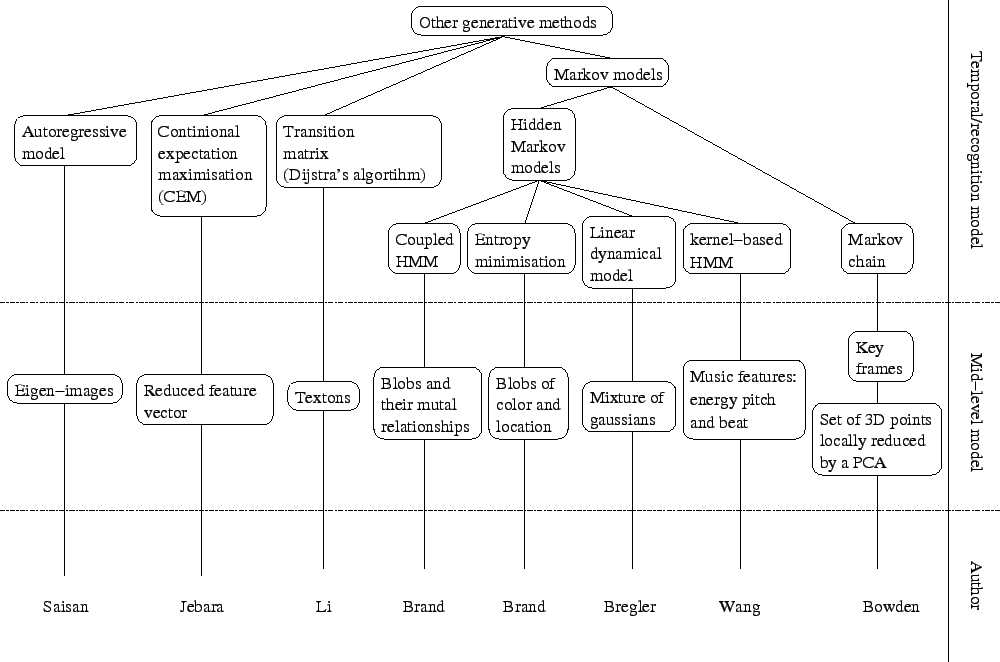
Other methods that use neither appearance model nor samples from original video sequences are described in this section. A tree representation of this part of the literature can be found in figure 2.7.

Figure 2.7: Other generative methods in behaviour modelling.

Saisan et al. [84] use autoregressive models to recognise dynamic textures such as waterfalls, smoke, waves or fire. After subsampling and reduction of the frames of the video sequences, a principle component analysis or an independent component analysis is applied to the set of frames to reduce their dimensionality. The dynamics of the process are then learnt from the reduced data in such a way that it produces a canonical representation of the data. Several distances between canonical representations of autoregressive models are tested with both the independent component analysis and the principle component analysis representation. Best results were obtained with the principle component analysis using Martin's distance [66]: a recognition rate of $89.5\%$ has been achieved on a database of 200 dynamic textures.

Jebara and Pentland [48] propose an Action-Reaction Learning (ARL) in order to synthesise human behaviour. After using colour classification [47], blobs corresponding to the positions and orientations of the head and hands of a user are extracted using an expectation maximisation algorithm. A Kalman filter is used to improve the tracking of the blobs. A time series approach is used to map past to future. A window is chosen to represent the 128 previous frames (about 6.5 seconds of video). This gives a series of vectors of dimension 3840, that is 15 parameters for the blobs by 2 individuals by 128 frames. The dimensionality of these vectors are then reduced using a principle component analysis to form a 40 parameter vector. The most recent vector and the most recent velocity are then concatenated to this vector to form the input vector of the system. This input vector encodes the past action of each frame. The corresponding output vector is given by the 30 dimensional vector representing the current frame. The conditional expectation maximisation algorithm [49] is then used to find the probability of the location and direction of the blobs given the compressed past vector. After having observed the interaction between two users, the system is the able to display blobs that interact in a meaningful sense with a single user.

Bowden [11] models a sequence of captured 3D body movements and learns the associated motions. The set of 3D points is first modelled by a principle component analysis and then clustered in the component space. Each cluster is then modelled separately by a principle component analysis, in contrast with the global principle component analysis usually used in point distribution models. Each principle component models a part of the trajectory of the 3D points. The motion of the points is then modelled by a Markov chain that gives the probability of moving from one centre of the clusters to another one. New motions can be synthesised by generating a sequence of cluster centres to be used as key frames. A smooth trajectory of 3D points is obtained by interpolating between the key frames.

Li et al. [58] use textons to model behaviour of 3D skeletons. The dimension of the 3D capture data is first reduced by a singular value decomposition. They automatically segment a stream of 3D capture data to find what they call a texton. It represents an action or a part of an action performed by the actor in the 3D capture data sequence. A texton is modelled by an autoregressive model of hidden state variables that are projected back onto the space of 3D skeletons (this is similar to [84]). A maximum likelihood framework is used to segment the stream. Considering the transition points and the labels of the segments as hidden variables, an expectation maximisation algorithm [27] is used to solve the maximum likelihood problem. Once each texton is modelled, a transition matrix is created by counting the frequencies of the textons. Generating textons is only valid locally and the generation quickly deviates from a realistic behaviour. In order to overcome the problem, Li et al. constrains the generation of textons by specifying the starting and ending two frames during the generation. This is done by solving a system of linear equations, but only copes with given realistic poses. Otherwise the generated texton becomes unrealistic (this is similar to the over-constrained problem that we describe in section 7.4.2). A new sequence can then be generated by sampling new textons accordingly to the transition matrix and constraining any new texton to begin with the last generated frame. Finally, new sequences can also be generated by providing the starting and ending two frames. The optimal sequence of textons used is computed from the transition matrix using Dijkstra's algorithm [24].

Bregler [15] uses a hierarchical framework to recognise human dynamics in video sequences of people running. The framework can be decomposed into four steps: the raw sequence, a model of movements by mixture of Gaussians, a model of linear dynamics and a model of complex movements. The basic movements are modelled with a mixture of Gaussians using the expectation maximisation algorithm on a probabilistic estimation of the motion based on the gradient of the raw sequence. The Gaussians are then grouped into blobs. Each blob is tracked by a Kalman filter. The Kalman filter is chosen to model a movement with constant velocity because we do not know the specific motion of each blob. A cyclic hidden Markov model is then used to model the high level complexity of motion. The hidden Markov model is trained with an iterative procedure that requires an initial guess of the model parameters. This guess is obtained by dynamic programming and is fine-tuned by the procedure.

Brand and Kettnaker [13,54] introduce a new framework to learn hidden Markov models. Instead of the conventional Baum-Welch algorithm based on expectation maximisation, their algorithm is based on entropy minimisation. In practice, the M-step of the expectation maximisation algorithm is modified to minimise the entropy of the data, the entropy of the model distribution and the cross-entropy between the expected statistic of the data and the model distribution instead of maximising the likelihood. This method gives deterministic annealing within the expectation maximisation framework and turns it into a quasi-global optimiser. It has been tested on the learning of the activity of an office. Contrary to the conventional way of learning hidden Markov model, this algorithm gives a learnt model with meaningful hidden states such as: enter/exit activity, whiteboard writing, use of the phone or use of the computer. The transition matrix obtained is sparse and thus shows that the structure of the scene has been discovered. It is also shown that it is more successful in detecting abnormal behaviour.

Brand et al. [14] claim that classical hidden Markov models are not good at correctly modelling interactions. Indeed, the Markov assumptions used to construct the models are false for most interaction data. They do not encode time properly. They investigate a new model called coupled hidden Markov model (see figure 2.8(c)) where a state does not depend only on the previous state but on several previous states that are intuitively modelling the state of each actor of the interaction. They use the entropy minimisation algorithm previously described to train these coupled hidden Markov models [12]. They compare the classical hidden Markov model (see figure 2.8(a)), a linked hidden Markov models introduced by Saul and Jordan [85], which models balance between actors of an interaction (see figure 2.8(b)), and the coupled hidden Markov models (see figure 2.8(c)). The data set used is a set of Thai Chi gestures. It is shown that coupled hidden Markov models outperform the two other models. Linked hidden Markov models were generally better than classical hidden Markov models except for particular moves where the dynamics of the gesture cannot be capture correctly.

Figure 2.8: Graphical representation of HMM, linked HMM, coupled HMM and cyclic HMM. Figure 2.8(a) describes the representation of hidden Markov models. The states are linked with the conditional probabilities of going to a state given we were in a previous state. A state represents both actors of an interaction. The hidden Markov chain is presented unrolled in time. Figure 2.8(b) represents the linked hidden Markov chains where states are also linked with the joint probability of both actors being in the linked states. Figure 2.8(c) represents the coupled hidden Markov model were the states depends on the previous states of both actors in the interaction. Finally, figure 2.8(d) models cyclic motions. The hidden states are temporally linked, each one of them representing a part of a cyclic motion.

Wang et al. [98] synthesise dynamic sequences of a virtual conductor using a music track as an input to the system. The joint input and output distribution sequence is modelled by a kernel-based hidden Markov model (KHMM). The joint probability of the input and output given the hidden state is estimated by a mixture of Gaussians. The parameters of this mixture are computed using the EM algorithm [27]. Features such as energy, pitch and beat are used as an input, and positions and velocities of 15 markers on the conductor body are used as an output. The training data set is acquired from a real conductor performing conducting gestures on several types of music. Once the model has been trained, the probability of the output given the input can be computed using a maximum likelihood framework. The resulting output sequence exhibit the global dynamics of the music while preserving the fine details of the conducting gestures.