Statistical shape models represent the structure of an object using a set of landmark points. They are trained using manually annotated images. The manual labelling is a way of including human knowledge into a learning mechanism. Figure 3.2 shows an example of hand labelled image. The shape is described by a vector ![]() that contains the coordinates of each point of the shape.
that contains the coordinates of each point of the shape.
![\includegraphics[width=145mm,keepaspectratio]{anot.eps}](img31.png)
|
The first step of the statistical shape model is to align the shapes found in the training set. This is done by an approach called Procrustes analysis [29]. This algorithm is iterative and reduces the sum of the distances between each shape to the mean shape. On its completion, all the shapes have the same centre of gravity, scale and orientation.
The variation in shape is then estimated by applying a principle component analysis (PCA) to the vectors representing the aligned shapes. The mean of these ![]() vectors is computed:
vectors is computed:
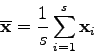 |
(2) |
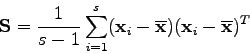 |
(3) |
In order to decrease the dimensionality of the data, the eigenvectors corresponding to the ![]() largest eigenvalues are chosen, as they explain most of the variation of the dataset. A threshold
largest eigenvalues are chosen, as they explain most of the variation of the dataset. A threshold ![]() is previously chosen (usually
is previously chosen (usually ![]() or
or ![]() ). We then compute
). We then compute ![]() by taking the minimum integer where the equation:
by taking the minimum integer where the equation:
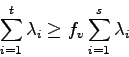 |
(4) |
If we define
![]() , each vector
, each vector ![]() in the training set can be approximated by:
in the training set can be approximated by:
| (5) |
| (6) |
![]() describes the shape
describes the shape ![]() . The approximation of the shape
. The approximation of the shape ![]() can be reconstructed with only
can be reconstructed with only ![]() , given that we know the model (that is,
, given that we know the model (that is,
![]() and
and ![]() ). Constraining the model to small variations allows it to generate only shapes that are similar to the training shapes. This can be done either by restricting the elements
). Constraining the model to small variations allows it to generate only shapes that are similar to the training shapes. This can be done either by restricting the elements ![]() of
of ![]() to vary between bounds (for instance
to vary between bounds (for instance
![]() ) or by constraining
) or by constraining ![]() to be in a hyper-ellipsoid:
to be in a hyper-ellipsoid:
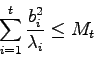 |
(7) |
Figure 3.3a shows the first mode of variation of the model built on images of annotated faces.
 |