| (12) |
The aim of active appearance search is to find the parameters of the statistical appearance model that best fits it to a previously unseen image. The active appearance model search is based on the idea that the reconstruction of the image should be close to the original image. We aim to minimise the difference between the target image and the synthesis of the model.
This minimisation is done by iteratively improving a current estimate of the parameters of the model. For each step, the algorithm uses the difference between the target image and the synthesis of the model using the current estimate of the parameters. This difference is represented in a residual vector:
| (12) |
 |
We seek to minimise the square of the norm of ![]() :
:
We model the residuals by assuming a local linear relationship between the parameters and the residuals:
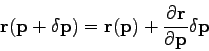 |
(14) |
For each step, we select
![]() which minimises
which minimises
![]() . We require
. We require
![]() for
for
![]() .
.
We have:
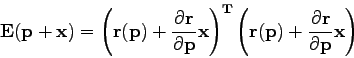 |
(15) |
So:
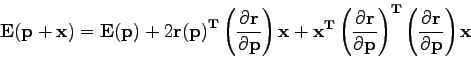 |
(16) |
This gives us the derivative of ![]() with respect to
with respect to ![]() :
:
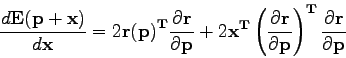 |
(17) |
By equating
![]() to zero, we obtain:
to zero, we obtain:
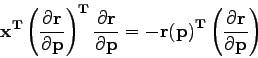 |
(18) |
That is:
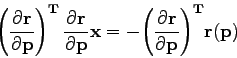 |
(19) |
So
![]() can be computed using the formula:
can be computed using the formula:
| (20) |
where:
Computing ![]() at each iteration is computationally expensive. We assume that this matrix can be considered approximatively constant, since it is computed in a normalised reference frame. So we compute it once from our training data. The equation becomes:
at each iteration is computationally expensive. We assume that this matrix can be considered approximatively constant, since it is computed in a normalised reference frame. So we compute it once from our training data. The equation becomes:
| (22) |
Given this model of image differences, we generate displacements ![]() around the optimal value for training images, one parameter at a time, in order to find the corresponding
around the optimal value for training images, one parameter at a time, in order to find the corresponding
![]() by synthesis and image difference. This gives us a set of pairs
by synthesis and image difference. This gives us a set of pairs
![]() . Those can be used to approximate the matrix
. Those can be used to approximate the matrix
![]() by averaging and combining with a normalised Gaussian kernel
by averaging and combining with a normalised Gaussian kernel ![]() to smooth the result:
to smooth the result:
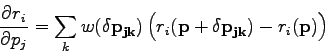 |
(23) |
where
![]() is the
is the ![]() displacement of the parameter
displacement of the parameter ![]() . The matrix
. The matrix ![]() can then be computed using equation 3.20.
can then be computed using equation 3.20.
Once the relationship between differences of parameters and differences of intensities in the images is computed, we can derive a search algorithm in order to locate the face. The search algorithm is summarised on figure 3.7.
Figures 3.8 and 3.9 show an example of the application of this algorithm.
 |
 |