A spatiotemporal model

In order to be able to keep track of the timing information, we need to extract the times for each point in a resampled pathlet . The pathlets are resampled so that the length of the resampled pathlet is constant between successive points. This process does not take the original timing into account. As we do not know the exact time for each point of the resampled pathlet, we linearly interpolate the time with the length of the curve for each segment of $1/25$ seconds (the time between points on the original pathlet).

Let $\bf\delta$ be the vector containing the time to reach each point of a resampled pathlet $s$. The new model of pathlet is the concatenation of the points of the resampled pathlet as well as the times to reach those points from the beginning of the pathlet. A pathlet is now represented by the vector $\left( {\bf s}^T , {\bf\delta}^T \right)^T$.

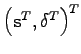Thus, the spatiotemporal model of a pathlet group becomes a linear combination of pathlets extended with timings. Each pathlet from a group is modelled by the equation:

$$\left(\begin{array}{c} {\bf s} \\ {\bf\delta} \end{array}\r... ...a} \end{array}\right) +{\bf Q_{s,\delta} } {\bf b_{s,\delta} }$$ (30)

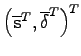where $\left(\overline{\bf s}^T,\overline{\bf\delta}^T\right)^T$ is a vector representing the mean pathlet of the group along with these timings, 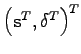${\bf Q_{s,\delta} }$ is a matrix computed by the principal component analysis and describing how the data varies and ${\bf b_{s,\delta} }$ is the vector of parameters for that particular pathlet. The probability density function of the set of parameters ${\bf b_{s,\delta} }$ is modelled by a Gaussian, by computing the mean and variance of ${\bf b_{s,\delta} }$ for all pathlets $\left( {\bf s}^T , {\bf\delta}^T \right)^T$ in the group.

Generation of pathlets is therefore a simple sampling from the distribution of ${\bf b_{s,\delta} }$. Applying equation 5.6 gives a pathlet $\bf s$ which is then resampled using cubic splines, and timing information $\bf\delta$. The points are resampled to correspond to times multiples of $\frac{1}{25}$ second. We linearly interpolate the time between two generated points and the length of the cubic spline curve between the points.

In some rare occasions, two consecutive generated points might have timings that are going backwards in time. This can occur because we use a (symmetric) Gaussian to represent strictly one sided (i.e. $\delta \geq 0$) data. Sampling from such a distribution can occasionaly gerenate negative values. We could of course have used a one sided probability distribution function such as the gamma distribution, but we could not easily account correlations with the spatial variables. Instead when sampling, we simply discard the generated pathlet and sample a new value for $\bf b_{s,\delta}$ from its probability distribution, to generate a new pathlet. This has also the advantage of eliminating some outlier pathlets that might have been generated without the timing model.