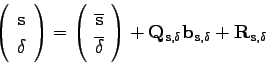The spatiotemporal model with linear residuals

When generating several pathlets in sequence, one needs the output to be smooth. However, by concatenating generated pathlets, the ends of the successive pathlets might not match. In order to avoid this problem, we extend the spatiotemporal to:

$$\left(\begin{array}{c} {\bf s} \\ {\bf\delta} \end{array}\r... ... +{\bf Q_{s,\delta} } {\bf b_{s,\delta} } +{\bf R_{s,\delta} }$$ (31)

where $\bf R_{s,\delta}$ represents the residuals.

In this work, we assume a linear spatial model for the residuals. It can be computed given the last point of the previous pathlet.

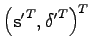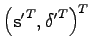We first generate a pathlet $\left( {\bf s'}^T, {\bf\delta'}^T \right)^T$ in the same way we do using the spatiotemporal model. We want the first point of this pathlet to match the previous pathlet. Let's call ${\bf e }$ the vector that translates the first point of $\left( {\bf s'}^T, {\bf\delta'}^T \right)^T$ into the last point of the previous pathlet. In order to obtain 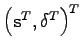$\left( {\bf s}^T , {\bf\delta}^T \right)^T$, we keep the timings and translate the points of $\bf s'$ so that:

$$s_{ik}={s'}_{ik}+\frac{\sum_{j=i}^{N-1} \delta_j}{\sum_{j=1}^{N-1} \delta_j} e_k$$ (32)

where $e_k$ is the $k^{th}$ coordinate of $\bf e$, $s_{ik}$ is the $k^{th}$ coordinate of the $i^{th}$ point in the pathlet $\bf s$, ${s'}_{ik}$ is the $k^{th}$ coordinate of the $i^{th}$ point in the pathlet $\bf s'$ and $\delta_j$ is the $j^{th}$ coordinate of $\bf\delta$. Figure 5.10 is an illustration of the application of equation 5.9.

Figure 5.10: Linear model of residuals. The first point of the current pathlet is moved to match the last point of the previous pathlet.

This generating process gives a new pathlet that begins at the end of a previously generated pathlet, thus generating a more continuous overall trajectory. However, this method is only valid if ${\bf e }$ is small. A large translation of points can generate an unrealistic pathlet. In practise, this problem of generation happens if an unlikely sequence of pathlets is generated by the model of temporal relationship between the pathlet models, described in chapter 6.