Results of clustering based on dynamic time warping and normalised cut

This section presents the pathlet groups extracted from original trajectories. The normalised cut algorithm has been used for the grouping while the dynamic time warping algorithm has been used for the similarity measure.

Tables 5.2 and 5.3 show pathlet groups extracted from the trajectory T1.

Table 5.2: Pathlet groups for trajectory T1 (groups 1 to 15) based on dynamic time warping and normalised cut clustering. For each group, the nodes are drawn in the upper figure with the pathlets forming that group. Using the pathlet model, one hundred generated pathlets are drawn in the lower figure.

pathlet groups of trajectory T1
Group 1	Group 2	Group 3	Group 4	Group 5
Group 6	Group 7	Group 8	Group 9	Group 10
Group 11	Group 12	Group 13	Group 14	Group 15

Table 5.3: Pathlet groups for trajectory T1 (groups 16 to 25) based on dynamic time warping and normalised cut clustering. For each group, the nodes are drawn in the upper figure with the pathlets forming that group. Using the pathlet model, one hundred generated pathlets are drawn in the lower figure.

pathlet groups of trajectory T1
Group 16	Group 17	Group 18	Group 19	Group 20
Group 21	Group 22	Group 23	Group 24	Group 25

For each pathlet group, the nodes extracted from the original trajectory are shown with black dots; the pathlets that form the group are drawn between the nodes. The nodes have been generated using algorithm A4, as previously illustrated in table 5.1 page .

Below those pictures, we represent the pathlet model by the generation of one hundred random pathlets. This is done by sampling pathlets from the group, with a Gaussian distribution around the mean pathlet, in order to represent the variance of that group. Only dots representing the positions of the generated points are shown for the reader to appreciate the modelling of timings.

Note that one can find four different types of pathlet models:

• pathlet models that model properly the variations observed with several similar pathlets (models learnt from groups 3, 9, 11 or 21 in tables 5.2 and 5.3, for instance).
• pathlet models that have been build with only one pathlet. Those models can only generate one pathlet since the variance in its training set of pathlets is null; 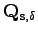$\bf Q_{s,\delta}$ from equation 5.6 is therefore the null matrix (models learnt from groups 20 and 25 in table 5.3, for instance).
• pathlet models that have been built with an outlier in their training set of pathlets (models learnt from groups 2, 5, 6, 10, 12 or 24 in tables 5.2 and 5.3, for instance).
• pathlet models which have been trained on pathlets that do not look totally similar (models learnt from groups 14 and 22 in table 5.2 and 5.3, for instance).

Similar type of pathlet models can be observed when applying the algorithms to trajectory T2 (tables 5.4 and 5.5) and trajectory T3 (table 5.6).

For instance for trajectory T2, the pathlet models corresponding to groups 3, 14 or 21 have been learnt on a set of pathlets containing outliers. The groups 1, 8 , 23, or 25 are correctly modelled, while the pathlet models corresponding to groups 12 or 13 have been built using only one pathlet. Finally pathlet models corresponding to the groups 6, 19 or 26 have been learnt on a set of pathlets that do not look similar to each other.

Finally, the same types of pathlet models can be observed when extracting pathlet groups form the trajectory T3 (see table 5.6).

Note that tables 5.2, 5.3, 5.4, 5.5 and 5.6 shows all the possible generated pathlets. They include the pathlets that have been generated with negative timings. This often occurs where the pathlet groups contain outliers. For instance the pathlet model corresponding to group 5 extracted from trajectory T1 can generate such impossible pathlets. Figure 5.12 shows pathlets generated from the pathlet model of group 5 extracted from the trajectory T1. Pathlets generated with negative timings are circled with a dotted circle. As mentioned in section 5.3.2, pathlets that have timings going backward in time are discarded and new pathlets are generated instead. We can see that this rejection of impossible pathlets improves the output of the pathlet model. However the model still remains weak since it can generate other unlikely pathlets.

Figure 5.12: Generation of pathlets with negative timings. A hundred pathlets have been generated from the pathlet model learnt from the pathlet group 5 extracted from trajectory T1. The pathlets with negative timings have been circled with a dotted circle. In practice we ignore such pathlets and sample again.

Table 5.4: Pathlet groups for trajectory T2 (groups 1 to 15) based on dynamic time warping and normalised cut clustering. For each group, the nodes are drawn in the upper figure with the pathlets forming that group. Using the pathlet model leant from that group, one hundred generated pathlets are drawn in the lower figure.

pathlet groups of trajectory T2
Group 1	Group 2	Group 3	Group 4	Group 5
Group 6	Group 7	Group 8	Group 9	Group 10
Group 11	Group 12	Group 13	Group 14	Group 15

Table 5.5: Pathlet groups for trajectory T2 (groups 16 to 26) based on dynamic time warping and normalised cut clustering. For each group, the nodes are drawn in the upper figure with the pathlets forming that group. Using the pathlet model learnt from that group, one hundred generated pathlets are drawn in the lower figure.

pathlet groups of trajectory T2
Group 16	Group 17	Group 18	Group 19	Group 20
Group 21	Group 22	Group 23	Group 24	Group 25
Group 26

Table 5.6: Pathlet groups for trajectory T3 (groups 1 to 9) based on dynamic time warping and normalised cut clustering. For each group, the nodes are drawn in the upper figure with the pathlets forming that group. Using the pathlet model learnt from that group, one hundred generated pathlets are drawn in the lower figure.

pathlet groups of trajectory T3
Group 1	Group 2	Group 3	Group 4	Group 5
Group 6	Group 7	Group 8	Group 9

Ideally, we prefer to have pathlet models that model the original data properly. We want to avoid pathlet models modelling outliers as well as those modelling pathlets that do not look similar to each other. The two other types of pathlet models are able to model properly the original data.

Pathlet models built from pathlet groups that only contain one pathlet reproduce exactly the pathlet they have learnt. Since we want to avoid using original frames to create the output video of our system, we would like to avoid such models. However, we cannot discard those groups. Since we cannot generalise from a group of pathlets with only one example, we have to copy them to be faithful to the original data.