Laplace's law of succession

This is Laplace's first attempt to estimate probabilities of events occurring consecutively in a sequence. Its goal is to estimate the probability of an event occurring $n+1$ times in succession given that the event occurred $n$ times in succession.

The law can be found using the following reasoning:

Suppose that we have $N+1$ coins that we label from $0$ to $N$. Each coin has a different probability of landing heads up. The coin $i$ lands heads up with a probability of $i/N$. We assume that the coins can be chosen with a uniform probability. We can then choose a coin and toss it again and again.

The probability that the first $n$ toss are all heads for this particular coin is given by:

$$P(n\: heads\vert coin=i)=\left(\frac{i}{N}\right)^n$$

So, the probability of observing $n$ heads in a row in this experiment is:

$$F_{N,n}=P(n\: heads)=\sum_{i=0}^NP(coin=i)\cdot P(n\: heads\vert coin=i)=\frac{1}{N+1}\sum_{i=0}^N\left(\frac{i}{N}\right)^n$$

Furthermore:

$$P(n+1\: heads\vert n\: heads)\cdot P(n\: heads) = P(n\: heads\vert n+1\: heads)\cdot P(n+1\: heads)$$

If the first $n+1$ toss are all heads, the first $n$ toss are all heads too, so

$$P(n\: heads\vert n+1\: heads)=1$$

and

$$P(n+1\: heads\vert n\: heads)=\frac{F_{N,n+1}}{F_{N,n}}$$

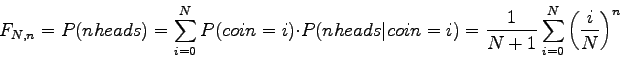
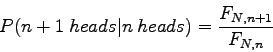
We want this to be true in general and not only for a finite number of possible probabilities $\left\{\frac{i}{N}\right\}_i$. In order to do that, we have to take an infinite number of coins with probabilities describing the possible range of probabilities $\left[0,1\right]$. The probability we are looking for becomes:

$$P(n+1\: heads\vert n\: heads)=\lim_{N \to \infty} \frac{F_{N,n+1}}{F_{N,n}}$$

The properties of integrals give us:

$$\lim_{N \to \infty} F_{N,n}=\int_0^1x^n\:dx=\left[\frac{x^{n+1}}{n+1}\right]_0^1=\frac{1}{n+1}$$

So we can express the solution with this simple formula:

$$P(n+1\: heads\vert n\: heads)=\frac{n+1}{n+2}$$

This is a special case of the Laplace's law of succession. The key observation is that a uniform probability prior is required to apply the formula. In practice we do not know the distribution of the priors. Furthermore, the priors may depend on the context, so we cannot compute them and thus we have to make a choice. It has also been proved (see [46] for instance) that the Laplace's formula is general and gives the same result with other forms of prior probabilities.

In our case, the formula can be extended and we can compute the probability of a sequence $s$ being sampled next given that we observed a sequence of $N_s$ sequences [46] . An estimate of the probability of the sequence $s$ is:

$$P(s)=\frac{n_s+1}{N_s+\vert\Sigma\vert}$$

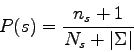
This way of estimating the probabilities was used by Ron et al. to train a variable length Markov model [81].