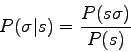One problem that arises when one deals with finite sequences is that of estimating the probabilities. The true underlying probability is not known. The probabilities must be estimated. We investigated several ways of estimating probabilities from sequences of letters (or pathlet models respectively). The details of the different laws of succession mentioned here can be found in [80].
We denote by ![]() the number of times the sequence
the number of times the sequence ![]() is observed as being a subsequence of the training sequence. The training sequence is supposed to represent the population of sequences we will have to deal with, that is samples from the probability distribution we want to model. We denote by
is observed as being a subsequence of the training sequence. The training sequence is supposed to represent the population of sequences we will have to deal with, that is samples from the probability distribution we want to model. We denote by ![]() the number of possible subsequences of size
the number of possible subsequences of size ![]() in the training sequence, that is:
in the training sequence, that is:
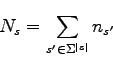
Furthermore, the conditional probability ![]() is by definition:
is by definition: