The natural law of succession

The natural law of succession presented in [81] is a more complex law of succession. It is based on the fact that simple sequences are more probable than complex sequences. The probabilities are then estimated using a more appropriate subset of the alphabet. Alphabets are usually large, and so natural sequences do not include all the elements of the alphabet. The number of possible subsequences found in the observed sequence is given by:

$$q=\left\vert\left\{s\vert s \in \Sigma^*, n_s>0\right\}\right\vert$$

The formula can then be derived as follow:

$$P(s)=\left\{\begin{array}{ll} \frac{n_s+1}{N_s+\vert\Sigma\ve... ...a\vert-q)(N_s^2+N_s+2q)} & {\rm otherwise} \end{array}\right.$$

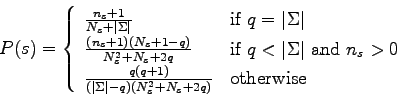
It has been proved both in theory and in practice that this law of succession outperforms the previous ones.

Unfortunately, from a practical point of view, the natural law of succession is too computationally expensive. Indeed, the computation of the formula requires the value of $q$. The computation of $q$ is done by counting the number of all sets of similar subsequences of any size in the observed sequence. Furthermore, the variable length Markov model learning algorithm uses extensively the estimation of observed probabilities. We cannot afford a loss of performance for this estimation so we will not consider the law of succession in the rest of this thesis.