The Matusita distance

The Matusita measure between two probability distributions $p$ and $q$ is given by:

$$D_{B}(p\Vert q)=\int \left(\sqrt{p(x)}-\sqrt{q(x)}\right)^2 \; dx = 2-2\int \sqrt{p(x)\cdot q(x)} \; dx$$

where $x$ describe the whole space again. The term 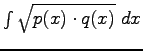$\int \sqrt{p(x)\cdot q(x)} \; dx$ is called the Bhattacharyya measure [1]. In our case the distance becomes:

$$D\left(\tilde{P}(\cdot\vert\sigma s)\Vert\tilde{P}(\cdot\vert... ...{\tilde{P}(\sigma'\vert\sigma s)\cdot\tilde{P}(\sigma'\vert s)}$$

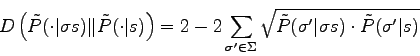
Thus:

$$Err(\sigma s,s)=2\tilde{P}(\sigma s) - 2\tilde{P}(\sigma s)\s... ...\sigma')\tilde{P}(s \sigma')}{\tilde{P}(\sigma s)\tilde{P}(s)}}$$

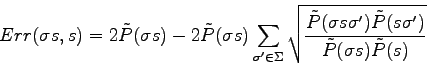
Unlike the Kullback-Leibler divergence, the Bhattacharyya term is symmetric and is invariant to scale in the case of two Gaussian probability density distributions. The Matusita measure inherits these properties.