In order to compare the two models, we need some measure of behavioural similarity between two video sequences. Our approach is to compare the distribution of the generated points in the parameter space with the distribution of points extracted from the original video sequence.
We construct two dimensional histograms to approximate the distribution of points in the parameter space for each pair of dimensions. We choose two dimensional histograms instead of ![]() dimensional histograms because we rarely have sufficient data to fill the latter, and because of the computational complexity of generating
dimensional histograms because we rarely have sufficient data to fill the latter, and because of the computational complexity of generating ![]() dimensional histograms.
dimensional histograms.
In order to compare the original and generated sequences of points using histograms, particular care has to be taken on the selection of the bin width used to compute those histograms. Indeed, a too large bin width will smooth the original data while a too small bin width will result in an over-fitting of the data. In order to solve this problem, and for reproducibility of the comparison method, we used Scott's rule to select the bin size [97]. The bin size for each dimension is given by the formula:
| (38) |
The two dimensional histograms of a reference and a generated set of points are then compared using a Bhattacharyya overlap
![]() , where
, where ![]() and
and ![]() are the dimensions used to compute the histograms.
are the dimensions used to compute the histograms.
![]() can be computed for each pair of dimensions
can be computed for each pair of dimensions ![]() . The final similarity measure
. The final similarity measure ![]() is computed by averaging the quantities
is computed by averaging the quantities
![]() using the formula:
using the formula:
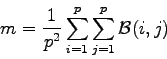 |
(39) |
![]() represents how close the point distributions of the generated and the reference sequences are. A value of
represents how close the point distributions of the generated and the reference sequences are. A value of ![]() corresponds to a perfect match of the distributions. A value of
corresponds to a perfect match of the distributions. A value of ![]() corresponds to two totally different distributions.
corresponds to two totally different distributions.
The facial behaviour models are assessed with respect to the original video sequence used to create those models. The distributions of points in the appearance parameter space should match with the original one if the model performs its task correctly.
Figures 8.5 and 8.6 show how this similarity measure can be applied to find the best generated trajectory in the appearance parameter space. Figure 8.5 shows a similarity result of ![]() while figure 8.6 shows a similarity result of
while figure 8.6 shows a similarity result of ![]() . Thus, the trajectory generated using our model has a greater similarity to the original trajectory than the trajectory generated using the autoregressive process. Our model performs better on this example. The next session describes the results obtained on the videos sequences V1, V2 and V3 introduced in section 4.3.
. Thus, the trajectory generated using our model has a greater similarity to the original trajectory than the trajectory generated using the autoregressive process. Our model performs better on this example. The next session describes the results obtained on the videos sequences V1, V2 and V3 introduced in section 4.3.
![\includegraphics[keepaspectratio]{comparp.eps}](img631.png)
|
![\includegraphics[keepaspectratio]{compmodel.eps}](img632.png)
|