![\begin{figure}\begin{center}
\subfigure[Camera looking forward]{\epsfysize =4c...
...ing upward]{\epsfysize =4cm \epsfbox{corrdemi.eps}
}
\end{center}
\end{figure}](img6.png) |
If the camera does not point in a fixed direction, the left wall is not always on the left-hand side of the image, and the right wall is not always on the right-hand side of the image. So in this case, the computation of an histogram of the image is not a solution.
A feature that can be computed is the angle of each of the lines which constitute the edges image, and a fixed direction. This idea has already been implemented in industrial robots such the plant-scale husbandry robot described in [31]. I have taken the vertical direction as the reference direction. It is good to notice that this feature is relevant only if the camera is pointing upwards or downwards, or only the upper or the lower part of the image is used. Indeed, in the edges image, a wall produces lines that form angles of different sign with the reference direction, depending on whether they are in the upper or the lower part of the image. However, if the camera is looking upwards, a wall generates lines that form angles of the same sign, and the other wall generates lines that form angles of the opposite sign. Indeed, all the strong lines seem to intersect at the end of the corridor. Figure 2.4 summarizes this.
![\begin{figure}\begin{center}
\subfigure[Camera looking forward]{\epsfysize =4c...
...ing upward]{\epsfysize =4cm \epsfbox{corrdemi.eps}
}
\end{center}
\end{figure}](img6.png) |
The problem is to calculate the angle of each line in the edges image. A common way to do this is to use a Hough transform. The Hough transform is described in [27]. The idea is to use an accumulator array which computes a strength for each line by a voting mechanism. This accumulator array is called Hough space. The dimension of the Hough space is defined by the number of geometric parameters we need to describe a pattern. These parameters describe the position or the scale of the pattern we want to recognize. We must be able to restore the original pattern using these parameters. Here, the pattern is a line, so the dimension of the Hough space is two.
I chose the two parameters as follows. The first one is the distance between the centre of the image and the line, and the second one is the angle between the line and the vertical. So each line in the edge-detected image corresponds to a unique point in the Hough space.
In order to find the lines that are correctly detected in an edge-detected image, each point that forms a line will vote for the corresponding parameters. So in the Hough space, a strong value correspond to a line which is well detected by the edge detector, that is, a solid line in the edge-detected image. We can then select the best lines by selecting the stronger values in the Hough space. This procedure is reliable and widely used in machine vision. Figure 2.5 shows an example of line detection using a Hough transform.
 |
In order to compute the Hough space, we have to change one of the two parameters, for each point in the original image. Knowing that the point we are dealing with is on the line, if we know the distance from the line to the centre, we can find the orientation of the line. It is the same if we know the orientation of the line, we can then find the distance between the line and the centre of the image. The second calculation seems to be simple, and so more efficient on a computer.
Figure 2.6 shows the situation when we try to compute the distance between a line and the centre of the image. ![]() denotes the point we are currently considering, and
denotes the point we are currently considering, and ![]() denotes the point located at the centre of the image.
denotes the point located at the centre of the image. ![]() denotes the distance between the line and
denotes the distance between the line and ![]() and
and
![]() is the normal to this line. The norm of this vector is
is the normal to this line. The norm of this vector is ![]() . Finally,
. Finally, ![]() denotes the angle between the vertical and the line. The aim is to compute
denotes the angle between the vertical and the line. The aim is to compute ![]() using the other parameters.
using the other parameters.
Let
![]() denotes the projection of
denotes the projection of
![]() on
on
![]() . We have:
. We have:
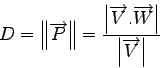


 |
So we can see that the distance ![]() can be easily computed if we know the angle
can be easily computed if we know the angle ![]() . Therefore I used the angle
. Therefore I used the angle ![]() as the varying parameter to compute the Hough space.
as the varying parameter to compute the Hough space.
The following algorithm is then used to compute the Hough space (the Hough space is represented by a two dimensional array in this algorithm):
compute the edge-detected image using an edge detector.
set all the elements of the array to 0.
for each point in the edge-detected image that is detected
as part of an edge, do:
for each angle between -90 degrees and 90 degrees, do:
* compute the distance between the line which goes
through the point and is directed by the angle,
and the centre of the image.
* in the array, increment the value of the element
labelled by the angle and the computed distance.
done.
done.
for each element of the array do:
* if the value of this element is greater than a fixed
threshold then the element is set to 1.
* set the element to 0 otherwise.
done.
return the array.
This procedure returns an array which is labelled by angles and distances. We can then use the angle by computing a histogram of the Hough space in the same manner as we computed histograms of images. We can also use the distance information by computing the corresponding histogram. Nevertheless, the distances seem to be less important than the angles. So I used wide stripes to compute the histogram for distances and small stripes to compute the histogram for angles. I then concatenate those two histograms and use it as input to a neural network.