Probabilistic Hough transform

Even if the formulas are pretty simple for the computation of the Hough space, it takes too much time to compute the Hough space of an image. If we use the algorithm described in section 2.2.2.2, it takes more than

seconds on a 486 PC to perform the Hough transform for a single image. This is too slow for usual operations. So I tried to optimize the computation using both practical and theoretical ideas.

First of all, I decreased the size of the Hough transform so that there are fewer labels and so the part of the algorithm which applies the threshold to the Hough space can be executed quicker. I also precomputed the sine and cosine functions because these functions use a lot of processing power. All the values needed were stored in an array. This array can be used to get values of sine and cosine of angles very quickly.

Another idea which is described in [17] is to slightly change the Hough transform in order to compute the parameters for fewer points. Indeed, it has been proved that computing parameters on only a fraction of the points is enough. The ratio depends of the complexity of the image, but a common ratio is $5\%$ - $15\%$ . This way of implementing the Hough transform is known as the probabilistic Hough transform.

The probabilistic Hough transform was implemented by choosing a ratio of $20\%$ to be sure to keep a decent amount of information. I have not chosen to take points randomly in the image, but take points randomly along lines. I have computed parameters for $20\%$ of the points for each line. This is more practical because the frame grabber provides the image line by line. So this avoids the problem of storing too many lines in memory. We can see in figure 2.7 that the thresholded Hough spaces does not look different for the Hough transform and the probabilistic Hough transform.

**Figure 2.7:** Difference between the Hough transform and the probabilistic Hough transform. The figure shows a Hough space and its thresholded version for both standard and probabilistic Hough transforms. Note the different threshold values.
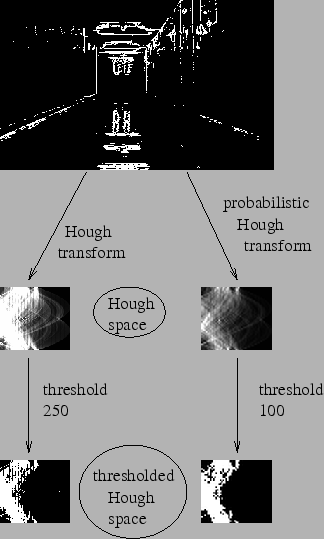$\begin{figure}\begin{center} \epsfbox{htetpht.eps} \end{center} \end{figure}$

We also notice that the thresholds are different because the peak values are not so strong in the probabilistic Hough space as in the standard Hough space. Indeed there are fewer points that can vote in the probabilistic Hough transform than in the standard Hough transform.