The gradient of the sum-of-square error function of a multi-layer Perceptron is calculated using the backpropagation algorithm. The propagation algorithm is a preliminary of the backpropagation algorithm.
In order to explain how these two algorithms works, I have to number the neurons from left to right beginning by the layer ![]() , then the layer
, then the layer ![]() , and so on. Let
, and so on. Let ![]() denote the weight of the link between neuron
denote the weight of the link between neuron ![]() and neuron
and neuron ![]() . Let
. Let ![]() denote the set of neurons whose output is an input of the neuron
denote the set of neurons whose output is an input of the neuron ![]() .
. ![]() is the potential of the neuron
is the potential of the neuron ![]() , and
, and ![]() is the returned value of the neuron
is the returned value of the neuron ![]() . Finally, let
. Finally, let ![]() denote the set of neurons whose set of inputs contains the output of the neuron
denote the set of neurons whose set of inputs contains the output of the neuron ![]() .
.
The propagation algorithm propagates an input vector ![]() through the network. It is used to compute the output of the neural network knowing the inputs and the weights:
through the network. It is used to compute the output of the neural network knowing the inputs and the weights:
For ![]() from
from ![]() to the number of neurons, do:
to the number of neurons, do:
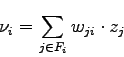
This algorithm computes the value of the potential of each neuron. These values are used by the backpropagation algorithm which computes the gradient of the sum-of-square error. It computes
![]() for each weights and for each example,
for each weights and for each example, ![]() , in the training set. The algorithm is based on the following factorization:
, in the training set. The algorithm is based on the following factorization:
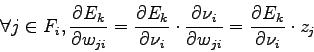
We know that ![]() denotes the desired output of the neural network if
denotes the desired output of the neural network if ![]() is the input vector. For the last neuron, we have:
is the input vector. For the last neuron, we have:
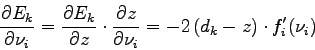
where ![]() is the number of a neuron located on the layer
is the number of a neuron located on the layer ![]() , and
, and ![]() is computed with the propagation algorithm. For the other neurons, we have:
is computed with the propagation algorithm. For the other neurons, we have:
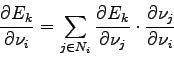
but:
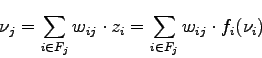
thus:
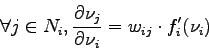
finally:
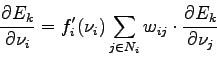
These computations can be summarized with the following algorithm :
For all couple of inputs/output in the training set, do:
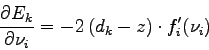
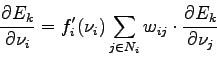
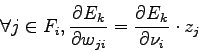
Two methods were used for the minimization of the error function. In a first stage, we try to approach a minimum of the error function using a gradient descent. In a second stage, we use a Quasi-Newton algorithm to find the minimum. The Quasi-Newton algorithm is only valid in a neighbourhood of the minimum. It has to be initialized with a point close to the minimum. That is why we have to use a gradient descent before using the Quasi-Newton algorithm. The next section describes these two minimization algorithms.