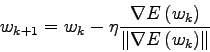The method of gradient descent is one of the most fundamental procedures for the minimization of a function 
of several variables. In order to find a minimum, we begin at random values for the variables, which gives us a point 
in the original space. We can then choose another point by moving in a direction 
. The new point must have an image that is smaller then the image of the previous point. We then move again in another direction that decrease the value of the function to find another point, and so on.
Using this idea we keep decreasing the value of the function until we found a minimum. For each iteration, the first step is to find the right direction. We have to choose a descent direction. As we know that the opposite of the gradient is the steepest descent direction, we can choose the direction 
for each point 
as follows:
A second step, which is harder to find, is the length of step along each direction . If the step is too big, the algorithm can diverge. If it is too small, the algorithm takes a long time to converge. Some choices like a step of
are proved to converge [18]. However, these methods are often slow. Here, our goal is only to get quickly close to a minimum. So we can take a step of
where 
is a constant. With this step, we are also sure that the algorithm will not diverge until a big number of steps because the distance between two points is less than 
.
So the algorithm becomes:
Choose a random point 
.
For 
from to a fixed number of iterations:
