As the former algorithm is slow, especially in the neighbourhood of a minimum, we need a more powerful algorithm to find the minimum quickly. The Quasi-Newton algorithm is based on the idea that a function looks like a quadratic function near its minimum. In the case of a quadratic function, we have :
In practice, the computation of the Hessian of ![]() is very slow, so the convergence speed of this algorithm is not really as good as it is supposed to be. It is usually better to approximate the Hessian matrix in order to find a good descent direction. The BFGS (Broyden, Fletcher, Goldfarb and Shanno) formula was used to approximate the Hessian [1]. The descent direction becomes:
is very slow, so the convergence speed of this algorithm is not really as good as it is supposed to be. It is usually better to approximate the Hessian matrix in order to find a good descent direction. The BFGS (Broyden, Fletcher, Goldfarb and Shanno) formula was used to approximate the Hessian [1]. The descent direction becomes:
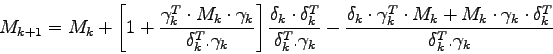
where
![]() and
and
![]() .
.
Even if the BFGS formula preserves positive definiteness, the computation of ![]() can lead to a matrix which is not positive due to rounding errors. So for each iteration, we must have
can lead to a matrix which is not positive due to rounding errors. So for each iteration, we must have
![]() . If it is not the case, we simply initialize
. If it is not the case, we simply initialize ![]() to the identity. It is proved that
to the identity. It is proved that
![]() tends to
tends to
![]() [18]. So the formula tends to produce the same result as the idea formula used for a quadratic curve.
[18]. So the formula tends to produce the same result as the idea formula used for a quadratic curve.
We also need the step for the update as it was the case in the gradient descent. Now this stage is more important because the minimization requires more precision near the minimum. However, the Quasi-Newton algorithm is not very sensitive to the step chosen. Thus, we can use a simple and efficient algorithm to choose this step like the Nash method [18].
These stages combined together lead to the following algorithm:
Initialize a tolerance factor ![]() between 0 and 1.
between 0 and 1.
Initialize a reduction factor ![]() between 0 and 1.
between 0 and 1.
Initialize the weights ![]() .
.
Initialize ![]() ,
,
![]() ,
, ![]() ,
,
![]() , and
, and ![]() .
.
Do:
If
![]() accept
accept ![]() .
.
Else compute
![]() and go back to step 1.
and go back to step 1.
Compute the new weights
![]() .
.
Compute the new gradient
![]() using
using
the back propagation algorithm.
Compute the new matrix ![]() using the BFGS formula.
using the BFGS formula.
Compute
![]() .
.
Initialize ![]() to
to ![]() again for the next iteration,
again for the next iteration,
and increment ![]() .
.
Until a certain number of iterations is reached or
until the weights are almost not changed
during the iteration (
![]() ).
).
In practice, this algorithm works fine with small networks. Indeed, the dimension of the matrix ![]() is the square of the number of weights of the network. So this matrix takes a lot of space in memory. This becomes a problem when we begin to use networks with a few thousand weights. In order to bypass this problem, we used a memoryless version of the Quasi-Newton algorithm [4]. This version is based on an approximation. In the BFGS formula,
is the square of the number of weights of the network. So this matrix takes a lot of space in memory. This becomes a problem when we begin to use networks with a few thousand weights. In order to bypass this problem, we used a memoryless version of the Quasi-Newton algorithm [4]. This version is based on an approximation. In the BFGS formula, ![]() is replaced by the unit matrix
is replaced by the unit matrix ![]() . We can then update the search direction using the formula:
. We can then update the search direction using the formula:
where ![]() and
and ![]() are two reals defined by:
are two reals defined by:
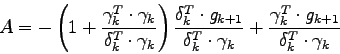
and
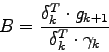
As we can see, this version of the Quasi-Newton algorithm only requires to store vectors and no matrix. So if ![]() is the number of weights of the network, the memory storage used is
is the number of weights of the network, the memory storage used is
![]() instead of
instead of
![]() .
.