 |
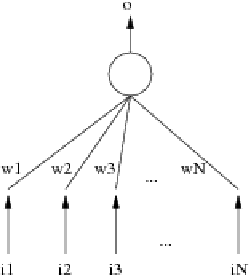
A Pattern Associator is a neural network with only one layer of neurons. This architecture was only used with one neuron because we only needed one output. The architecture used is shown in figure 2.10:
 |
The output of the Pattern Associator is computed using the formula:
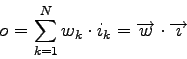
where ![]() is the current output generated by the Pattern Associator,
is the current output generated by the Pattern Associator, ![]() the corresponding expected value,
the corresponding expected value,
![]() the weights at the current iteration,
the weights at the current iteration,
![]() the current inputs and
the current inputs and ![]() a constant called learning rate. The learning rate may vary from one iteration to another. Considering the same arguments as the multi-layer Perceptron, the following formula was used:
a constant called learning rate. The learning rate may vary from one iteration to another. Considering the same arguments as the multi-layer Perceptron, the following formula was used:
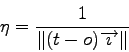
If the training examples are linearly separable, the Pattern Associator converges [19]. Furthermore, another advantage of the Pattern Associator is its low memory consumption. Each learning step, that is each application of the update formula, only requires the current inputs
![]() and the current target
and the current target ![]() . It is not necessary to store all the former training values. This avoids all the memory problems we had with the multi-layer Perceptron.
The update formula is also simple. It does not require a lot of computing power. These points are key points in embedded systems. So the Pattern Associator is well suited for robotics, as soon as the training examples are linearly separable.
. It is not necessary to store all the former training values. This avoids all the memory problems we had with the multi-layer Perceptron.
The update formula is also simple. It does not require a lot of computing power. These points are key points in embedded systems. So the Pattern Associator is well suited for robotics, as soon as the training examples are linearly separable.