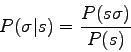The estimation of observed probabilities

One problem that arise when one deal with finite sequences is the problem of estimation of the probabilities. Indeed, the true underlying probability is not known. The probabilities must be estimated. I investigated several ways of estimating probabilities from sequences of letters (or prototypes respectively). The details of the different law of succession mentioned here can be found in [50].

In this section, we denote by $n_s$ the number of sequences $s$ observed as being a subsequence of the training sequence. The training sequence is supposed to represent the population of sequences we will have to deal with, that is the probability distribution we want to model. We also denote by $N_s$ the number of possible sequences of size $s$ in the training sequence, that is :

$$N_s=\sum_{s' \in \Sigma^{\vert s\vert}}n_{s'}$$

Note that $N_s$ can be computed by simply subtracting $\vert s\vert-1$ to the size of the training sequence.

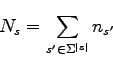
Furthermore, the conditional probability $P(\sigma \vert s)$ is by definition :

$$P(\sigma \vert s)=\frac{P(s \sigma)}{P(s)}$$

Therefore, we only need to estimate the probabilities of a sequence $s$. The different laws of succession give us such an estimate.