The Lidstone's law of succession is also commonly used in statistical practice. A parameter ![]() controls the formula of this law of succession given by:
controls the formula of this law of succession given by:
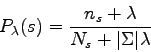
It has been shown that this class of probability estimates is in fact a linear interpolation between the maximum likelihood estimate given in section 5.3.3.2 and the uniform prior
![]() . Indeed, we can define a new constant
. Indeed, we can define a new constant ![]() by :
by :
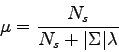
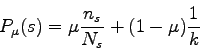
It is interesting to notice the particular cases of the Lidstone's law of succession :
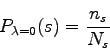
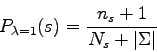
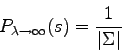
We can then see that the parameter ![]() has a meaning. It represents the trust we have in relative frequencies.
has a meaning. It represents the trust we have in relative frequencies. ![]() represents more trust in relative frequencies than the Laplace's law of succession while
represents more trust in relative frequencies than the Laplace's law of succession while ![]() represents less trust in relative frequencies. In practice,
represents less trust in relative frequencies. In practice, ![]() varies between
varies between ![]() and
and ![]() , a common value being
, a common value being
![]() [51].
[51].